一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(Ⅰ)求箱产品被用户接收的概率;
(Ⅱ)记抽检的产品件数为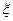 ,求
,求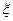 的分布列和数期望.
的分布列和数期望.
推荐套卷
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(Ⅰ)求箱产品被用户接收的概率;
(Ⅱ)记抽检的产品件数为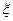 ,求
,求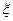 的分布列和数期望.
的分布列和数期望.