如图，正方形OABC的面积为9，点O为坐标原点，点B在函数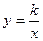
（k＞0，x＞0）的图象上，点P（m、n）是函数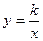（k＞0，x＞0）的图象上任意一点，
过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S.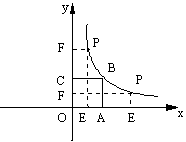
（1）求B点坐标和k的值；
（2）当S＝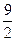
时，求点P的坐标。
，其中x满足
.
中，
，
，垂足为
.若
，
，求△
和△
中，
，
，
、
相交于点
，点
、
、
、
在同一直线上，且
．求证：
.
．
．相关知识点
推荐套卷
如图，正方形OABC的面积为9，点O为坐标原点，点B在函数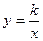
（k＞0，x＞0）的图象上，点P（m、n）是函数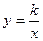（k＞0，x＞0）的图象上任意一点，
过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S.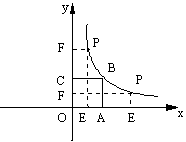
（1）求B点坐标和k的值；
（2）当S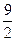＝时，求点P的坐标。
粤公网安备 44130202000953号