如图，在四棱锥P—ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD=AB=2，E是PB的中点，F是AD的中点．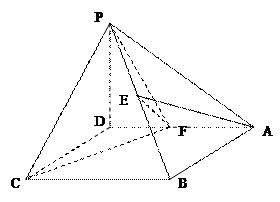
⑴求异面直线PD与AE所成角的大小；
⑵求证：EF⊥平面PBC ；
⑶求二面角F—PC—B的大小．.
相关试题
的终边与单位圆交于点
．
的值；
与
夹角为
，且
，求直线
的斜率．
的前
项和
.
满足
，
，求数列
.
，函数
的对称轴。
时,求
的最大值及对应的
值。
的夹角为
．
；（2）若
，求
的值．
的部分图像如图所示．
上的最大值和最小值．推荐套卷
如图，在四棱锥P—ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD=AB=2，E是PB的中点，F是AD的中点．
⑴求异面直线PD与AE所成角的大小；
⑵求证：EF⊥平面PBC ；
⑶求二面角F—PC—B的大小．.
粤公网安备 44130202000953号