(本题8分)某果园要用三辆汽车将一批水果从所在城市E运至销售城市F,已知从城市E到城市F有两条公路。统计表明:汽车走公路Ⅰ堵车的概率为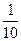 ,走公路Ⅱ堵车的概率为
,走公路Ⅱ堵车的概率为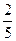 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响。
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响。
(Ⅰ)求甲、乙两辆汽车中恰有一辆堵车的概率。
(Ⅱ)求三辆汽车中至少有两辆堵车的概率。
推荐套卷
(本题8分)某果园要用三辆汽车将一批水果从所在城市E运至销售城市F,已知从城市E到城市F有两条公路。统计表明:汽车走公路Ⅰ堵车的概率为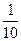 ,走公路Ⅱ堵车的概率为
,走公路Ⅱ堵车的概率为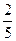 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响。
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响。
(Ⅰ)求甲、乙两辆汽车中恰有一辆堵车的概率。
(Ⅱ)求三辆汽车中至少有两辆堵车的概率。