如图，一条笔直的小路CA通向河边的一座凉亭A，小路与河边成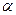
角（
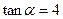），在凉亭北偏东45
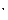方向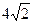
cm处的B处有一颗千年古树。现准备从小路的某点P处开挖新修一条直路P
D经过古树通向河边，两条路与河边围成的区域种上草坪。当开挖点P选在距凉亭多远处能使草坪占地面积最小？
是等腰直角三角形，
，
，
，延长
交
于
，连接
，求证：
，求与
垂直的一个单位向量的坐标。
，求
的
值
的图像，确定
的值
，并写出函数的解析式。
；
满足
，求数列
＞
。相关知识点
推荐套卷
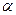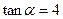如图，一条笔直的小路CA通向河边的一座凉亭A，小路与河边成角（），在凉亭北偏东45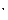方向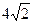cm处的B处有一颗千年古树。现准备从小路的某点P处开挖新修一条直路PD经过古树通向河边，两条路与河边围成的区域种上草坪。当开挖点P选在距凉亭多远处能使草坪占地面积最小？
粤公网安备 44130202000953号