在同一平面内有n条直线,任何两条不平行,任何三条不共点。
当n=1时,如图⑴,一条直线将一个平面分成两个部分;
当n=2时,如图⑵,两条直线将一个平面分成四个部分;
则:当n=3时,三条直线将一个平面分成 部分;
当n=4时,四条直线将一个平面分成 部分;
若n条直线将一个平面分成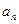 个部分,
个部分,
n+1条直线将一个平面分成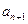 个部分。
个部分。
试探索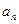 、
、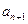 、n之间的关系。
、n之间的关系。
在同一平面内有n条直线,任何两条不平行,任何三条不共点。
当n=1时,如图⑴,一条直线将一个平面分成两个部分;
当n=2时,如图⑵,两条直线将一个平面分成四个部分;
则:当n=3时,三条直线将一个平面分成 部分;
当n=4时,四条直线将一个平面分成 部分;
若n条直线将一个平面分成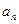 个部分,
个部分,
n+1条直线将一个平面分成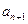 个部分。
个部分。
试探索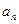 、
、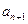 、n之间的关系。
、n之间的关系。