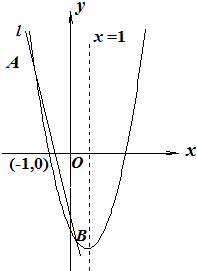如图,已知二次函数
的图象的对称轴为直线
,且与
轴有两个不同的交点,其中一个交点坐标为
.
(1)求二次函数的关系式;
(2)在抛物线上有一点
,其横坐标为-2,直线
过点
并绕着点
旋转,与抛物线的另一个交点是点
,点
的横坐标满足
,当
的面积最大时,求出此时直线
的关系式;
(3)抛物线上是否存在点
使
的面积与(2)中
的最大面积相等.若存在,求出点
的横坐标;若不存在说明理由.
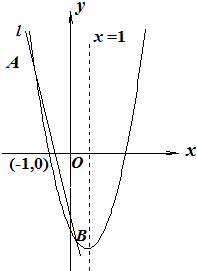
相关知识点
推荐套卷
如图,已知二次函数
的图象的对称轴为直线
,且与
轴有两个不同的交点,其中一个交点坐标为
.
(1)求二次函数的关系式;
(2)在抛物线上有一点
,其横坐标为-2,直线
过点
并绕着点
旋转,与抛物线的另一个交点是点
,点
的横坐标满足
,当
的面积最大时,求出此时直线
的关系式;
(3)抛物线上是否存在点
使
的面积与(2)中
的最大面积相等.若存在,求出点
的横坐标;若不存在说明理由.