甲盒有标号分别为1、2、3的3个红球；乙盒有标号分别为1、2、…、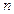
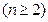
的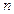个黑球，从甲、乙两盒中各抽取一个小球，抽到标号为1号红球和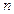号黑球的概率为
．
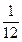（Ⅰ）求的值；
（Ⅱ）现从甲乙两盒各随机抽取1个小球，抽得红球的得分为其标号数；抽得黑球，若标号数为奇数，则得分为1，若标号数为偶数，则得分为0．求得分为2的概率．
相关试题
，函数
的图象的两相邻对称轴间的距离为
.
的值；
，
，求
的值；
，且
有且仅有一个实根，求实数
的值.
为偶函数，其图象上相邻的两个最低点间的距离为
．
的解析式；
求
的值．
与
是两个单位向量，其夹角为60°，且
，
的模；
，
，
，
∥
，试求满足
的
的坐标（O为坐标原点）。
的终边与单位圆交于点P（
，
）.
、
、
值；
的值.推荐套卷
甲盒有标号分别为1、2、3的3个红球；乙盒有标号分别为1、2、…、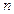
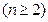
的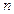个黑球，从甲、乙两盒中各抽取一个小球，抽到标号为1号红球和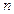号黑球的概率为．
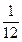（Ⅰ）求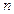的值；
（Ⅱ）现从甲乙两盒各随机抽取1个小球，抽得红球的得分为其标号数；抽得黑球，若标号数为奇数，则得分为1，若标号数为偶数，则得分为0．求得分为2的概率．
粤公网安备 44130202000953号