某学校为了丰富大课间自由活动的内容,随机选取本校部分学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”,根据收集整理到的数据绘制成以下统计图

根据以上信息,解答下列问题:
(1)学校采用的调查方式是 ,被调查的样本 容量是 。
容量是 。
(2)请补充完整图中的条形统计图和扇形统计图(百分率精确到1%);
(3)假如你绘制图中扇形统计图,你认为踢毽子对应的扇形圆心角应为 °(精确到1°).
(4)该校共有800名,请估计喜欢足球的学生人数。
相关知识点
推荐套卷
 ,求下列各式的值:
,求下列各式的值: ;
;  .
.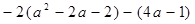 ,其中
,其中  .
. ,
,  ,
,  .
.
 轴上,OC边在
轴上,OC边在 轴上,且B点坐标为(4,3).动点M、N分别从点O、B同时出发,以1单位/秒的速度运动(点M沿OA向终点A运动,点N沿BC向终点C运动),过点N作NP∥AB交AC于点P,连结MP.
轴上,且B点坐标为(4,3).动点M、N分别从点O、B同时出发,以1单位/秒的速度运动(点M沿OA向终点A运动,点N沿BC向终点C运动),过点N作NP∥AB交AC于点P,连结MP.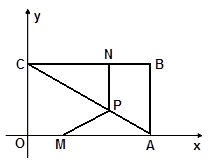
 的函数关系式;
的函数关系式; 粤公网安备 44130202000953号
粤公网安备 44130202000953号