. 本题满分13分
本题满分13分 甲乙二人用4张扑克牌
甲乙二人用4张扑克牌 分别是红桃2,红桃3,红桃4,方片
分别是红桃2,红桃3,红桃4,方片
4 玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放
玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放
回,各抽一张.
(I)设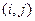 表示甲乙抽到的牌的数字,
表示甲乙抽到的牌的数字, 如甲抽到红桃2,乙抽到红桃3,记为
如甲抽到红桃2,乙抽到红桃3,记为 2,3
2,3
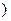 写出甲乙二人抽到的牌的所有情况;
写出甲乙二人抽到的牌的所有情况;
(Ⅱ)若甲抽到红桃3,则乙抽出的牌面数字比3大的概率是多少?
(Ⅲ)甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则,乙胜,你认为此游戏是否公平?请说明理由.
推荐套卷
. 本题满分13分
本题满分13分 甲乙二人用4张扑克牌
甲乙二人用4张扑克牌 分别是红桃2,红桃3,红桃4,方片
分别是红桃2,红桃3,红桃4,方片
4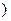 玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放
玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放
回,各抽一张.
(I)设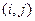 表示甲乙抽到的牌的数字,
表示甲乙抽到的牌的数字,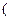 如甲抽到红桃2,乙抽到红桃3,记为
如甲抽到红桃2,乙抽到红桃3,记为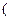 2,3
2,3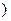
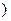 写出甲乙二人抽到的牌的所有情况;
写出甲乙二人抽到的牌的所有情况;
(Ⅱ)若甲抽到红桃3,则乙抽出的牌面数字比3大的概率是多少?
(Ⅲ)甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则,乙胜,你认为此游戏是否公平?请说明理由.