为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室.经预算,一共需要筹资30000元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊.
(1)筹委会计划,购买书刊的资金不少于购买书桌、书架等设施资金的3倍,问最多用多少资金购买书桌、书架等设施?
(2)经初步统计,有200户居民自愿参与集资,那么平均每户需集资150元.镇政府了解情况后,赠送了一批阅览室设施和书籍,这样,只需参与户共集资20000元.经筹委会进一步宣传,自愿参与的户数在200户的基础上增加了a%(其中a>0).则每户平均集资的资金在150元的基础上减少了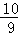 a%,求a的值.
a%,求a的值.