(6分)小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大
数减小数)大于或等于2,小明得1分,否则小亮得1分.你认为游戏是否公平?若公平,
请说明理由 ;若不公平,请你修改规则,使游戏对双方公平.
;若不公平,请你修改规则,使游戏对双方公平.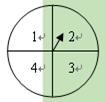
相关知识点
推荐套卷
(6分)小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大
数减小数)大于或等于2,小明得1分,否则小亮得1分.你认为游戏是否公平?若公平,
请说明理由 ;若不公平,请你修改规则,使游戏对双方公平.
;若不公平,请你修改规则,使游戏对双方公平.