在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题: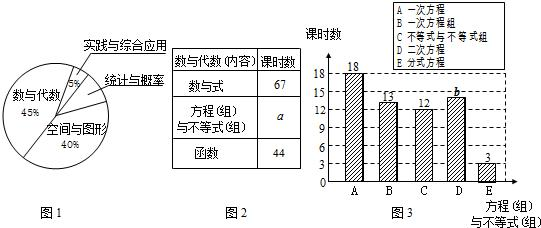
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
相关知识点
推荐套卷
在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?