（11·漳州）（满分8分）下图是2002年在北京举办的世界数学家大会的会标“弦图”，它既标志着中国古代的数学成就，又像一只转动着的风车，欢迎世界各地的数学家们．
请将“弦图”中的四个直角三角形通过你所学过的图形变换，在以下方格纸中设计另个两个不同的图案．画图要求：（1）每个直角三角形的顶点均在方格纸的格点上，且四个三角形到不重叠；（2）所设计的图案（不含方格纸）必须是中心对称图形或轴对称图形．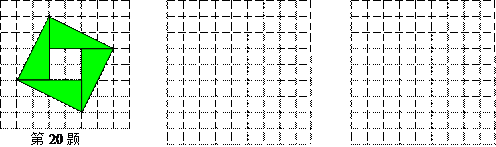
相关试题
，其中
其中
，求代数式
的值．下列数阵是由偶数排列成的：
（1）图中框内的四个数有什么关系（用式子表示）： ；
（2）在数阵中任意作一类似的框，如果这四个数的和为172 ，能否求出这四个数，怎样求？
（3）按数从小到大的顺序，上面数阵中的第100个数在第 排、第 列．
相关知识点
推荐套卷
粤公网安备 44130202000953号