2011年11月28日至12月9日,联合国气候变化框架公约第17次缔约方会议在南非德班召开,大会通过了“德班一揽子决议”(DurbanPackageOutcome),建立德班增强行动平台特设工作组,决定实施《京都议定书》第二承诺期并启动绿色气候基金,中国的积极态度赢得与会各国的尊重.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活逐渐成为人们的共识.某企业采用技术革新,节能减排.从去年1至6月,该企业二氧化碳排放量y1(吨)与月份x(1≤x≤6,且x取整数)之间的函数关系如下表:
月份x(月)
|
1
|
2
|
3
|
4
|
5
|
6
|
二氧化碳排放量y1(吨)
|
600
|
300
|
200
|
150
|
120
|
100
|
去年7至12月,二氧化碳排放量y2(吨)与月份x(7≤x≤12,且x取整数)的变化情况满足二次函数y2=ax2+bx(a≠0),且去年7月和去年8月该企业的二氧化碳排放量都为56吨.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1与x之间的函数关系式.并且直接写出y2与x之间的函数关系式;
(2)政府为了鼓励企业节能减排,决定对每月二氧化碳排放量不超过600吨的企业进行奖励.去年1至6月奖励标准如下,以每月二氧化碳排放量600吨为标准,不足600吨的二氧化碳排放量每吨奖励z(元)与月份x满足函数关系式z=x2﹣x(1≤x≤6,且x取整数),如该企业去年3月二氧化碳排放量为200吨,那么该企业得到奖励的吨数为(600﹣200)吨;去年7至12月奖励标准如下:以每月二氧化碳排放量600吨为标准,不足600吨的二氧化碳排放量每吨奖励30元,如该企业去年7月份的二氧化碳排放量为56吨,那么该企业得到奖励的吨数为(600﹣56)吨.请你求出去年哪个月政府奖励该企业的资金最多,并求出这个最多资金;
(3)在(2)问的基础上,今年1至6月,政府继续加大对节能减排企业的奖励,奖励标准如下:以每月二氧化碳排放量600吨为标准,不足600吨的部分每吨补助比去年12月每吨补助提高m%.在此影响下,该企业继续节能减排,1至3月每月的二氧化碳排放量都在去年12月份的基础上减少24吨.4至6月每月的二氧化碳排放量都在去年12月份的基础上减少m%,若政府今年1至6月奖励给该企业的资金为162000元,请你参考以下数据,估算出 m的整数值.
(参考数据:322=1024,332=1089,342=1156,352=1225,362=1296)
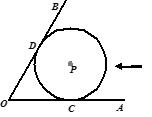
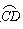 的长;
的长;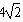 cm,求OC的长;
cm,求OC的长;
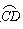 的长;
的长; cm,求OC的长;
cm,求OC的长;