(本小题满分 12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
(I)设所选5人中女医生的人数为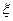 ,求
,求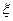
 的分布列及数学期望;
的分布列及数学期望;
(II)现从10名医生中的张强、李军、王刚、赵永4名男医生,李莉、孙萍2名女医生共6人中选一正二副3名组长,在张强被选中的情况下,求李莉也被选中的概率.
推荐套卷
(本小题满分 12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
12分)某医院计划从10名医生(7男3女)中选5人组成医疗小组下乡巡诊.
(I)设所选5人中女医生的人数为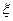 ,求
,求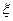
 的分布列及数学期望;
的分布列及数学期望;
(II)现从10名医生中的张强、李军、王刚、赵永4名男医生,李莉、孙萍2名女医生共6人中选一正二副3名组长,在张强被选中的情况下,求李莉也被选中的概率.