已知:抛物线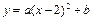
 的顶点为A,与x轴的交点为B,C(点B
的顶点为A,与x轴的交点为B,C(点B
在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由.
相关知识点
推荐套卷
已知:抛物线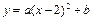
 的顶点为A,与x轴的交点为B,C(点B
的顶点为A,与x轴的交点为B,C(点B
在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由.