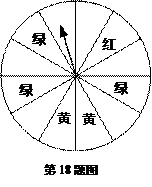
某学校决定:每周一举行的升旗仪式,若遇下雨或其它恶劣天气,学生就在教室
内参加升旗活动. 针对这一决定,校学生会在学生中作了一个抽样调查,调查问卷中有三个
选项:A、赞成;B、不赞成;C、无所谓.参加调 查的学生共300人,调查结果用条形统计
查的学生共300人,调查结果用条形统计
图表示﹙如图所示﹚.
(1)①请补全条形统计图;②还可以用哪类统计图表示调查结果?
(2)据此推测,全校2100位学生中,持“无所谓”观点的学生有多少?
(3)针对持B,C两种观点的学生,你有什么建议?
相关知识点
推荐套卷



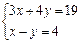 ;(2)化简:
;(2)化简: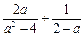 .
.
 x+150,
x+150, x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费).
x2元的附加费,设月利润为w外(元)(利润=销售额-成本-附加费). 的顶点坐标是
的顶点坐标是 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号