(本小题满分6分)“五·一”期间,某书城为了吸引读者,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元的书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.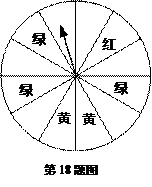
如果读者不愿意转转盘,那么可以直接获得10元的购书券.
(1)写出转动一次转盘获得45元购书券的概率;
(2)转转盘和直接获得购书券,你认为哪种方式对读者更合算?请说明理由.
相关知识点
推荐套卷
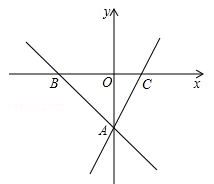
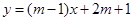

 与
与 的函数关系式;
的函数关系式; 时的函数值.
时的函数值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号