(本题6分)生活经验表明,靠墙摆放的梯子,当50°≤α≤70°时(α为梯子与地面所成的角),能够使人安全攀爬. 现在有一长为6米的梯子AB, 试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,
cos70°≈0.34,cos50°≈0.64)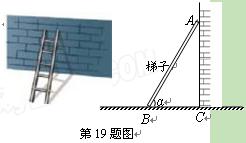
(本题6分)生活经验表明,靠墙摆放的梯子,当50°≤α≤70°时(α为梯子与地面所成的角),能够使人安全攀爬. 现在有一长为6米的梯子AB, 试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,
cos70°≈0.34,cos50°≈0.64)