请考生在（22）、（23）、（24）三题中任选一题作答，如果多答，则按做的第一题记分．作答时用2B铅笔在答题卡上把所选题目对应题号右侧的方框涂黑．
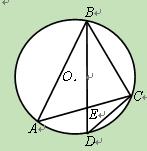
（22）（本小题满分10分）选修4—1：几何证明选讲。如图，⊙O是△
的外接圆，D
是的中点，BD交AC于E．
（Ⅰ）求证：CD
=DE·DB；
（Ⅱ）若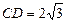
，O到AC的距离为1，求⊙O的半径
．
相关试题
为等差数列，且
的通项公式；
中,侧棱与底面垂直,
,
,点
分别为
和
的中点.
平面
;
的体积;
平面
.
中，角
所对的边分别是
，且
．
的大小；
，
，求
． 
三点共线，求实数
的值；
成立
为正数，求证：
相关知识点
推荐套卷
请考生在（22）、（23）、（24）三题中任选一题作答，如果多答，则按做的第一题记分．作答时用2B铅笔在答题卡上把所选题目对应题号右侧的方框涂黑．
（22）（本小题满分10分）选修4—1：几何证明选讲。如图，⊙O是△的外接圆，D
是的中点，BD交AC于E．
（Ⅰ）求证：CD=DE·DB；
（Ⅱ）若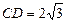，O到AC的距离为1，求⊙O的半径．
粤公网安备 44130202000953号