.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为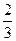 ,被乙小组攻克的概率为
,被乙小组攻克的概率为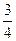 .
.
(1)设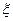 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求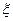 的分布列及
的分布列及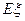 ;
;
(2)设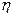 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件
在定义域内单调递增”为事件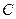 ,求事件
,求事件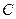 的概率.
的概率.
推荐套卷
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为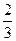 ,被乙小组攻克的概率为
,被乙小组攻克的概率为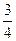 .
.
(1)设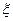 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求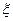 的分布列及
的分布列及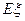 ;
;
(2)设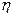 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件
在定义域内单调递增”为事件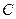 ,求事件
,求事件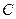 的概率.
的概率.