已知函数
在
处切线斜率为-1.
(I) 求
的解析式；
（Ⅱ）设函数
的定义域为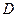
，若存在区间
，使得在
上的值域也是，则称区间为函数的“保值区间”
（ⅰ）证明：当
时，函数不存在“保值区间”；
（ⅱ）函数是否存在“保值区间”？若存在，写出一个“保值区间”（不必证明）；若不存在，说明理由.
相关试题
为锐角，且
，求
的值；
，求
的值.
是等差数列前
项和
，
.
的前
；
的前
.
中，
分别是角
的对边，
，且
∥
.
的大小；(2)求
的最小值.
.
；
的解集是
的解集.
的前n项和为Sn
，点（an，Sn）在直线y=2x-3n上．
；
的通项公式；
适合条件的项；若不存在，请说明理由．推荐套卷
已知函数在处切线斜率为-1.
(I) 求的解析式；
（Ⅱ）设函数的定义域为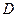，若存在区间，使得在上的值域也是，则称区间为函数的“保值区间”
（ⅰ）证明：当时，函数不存在“保值区间”；
（ⅱ）函数是否存在“保值区间”？若存在，写出一个“保值区间”（不必证明）；若不存在，说明理由.
粤公网安备 44130202000953号