已知二次函数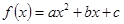
（其中
）满足下列3个条件：
①
的图象过坐标原点；
②对于任意
都有
成立；
③方程
有两个相等的实数根，令
（其中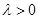
），
（1）求函数的表达式；
（2）求函数
的单调区间（直接写出结果即可）；
（3）研究函数在区间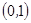
上的零点个数.
.
的最小值；
都有
，求实数
的取值范围.
，函数
，
，
，试讨论函数
的单调性．
（
），其中
，求函数
的极大值和极小值．
,
,设
．
的单调区间；
图像上任意一点
为切点的切线的斜率
恒成立，求实数
的最小值；
，求证
。推荐套卷
已知二次函数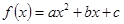（其中）满足下列3个条件：
①的图象过坐标原点；
②对于任意都有成立；
③方程有两个相等的实数根，令（其中），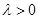
（1）求函数的表达式；
（2）求函数的单调区间（直接写出结果即可）；
（3）研究函数在区间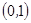上的零点个数.
粤公网安备 44130202000953号