某品牌电视生产厂家有 、
、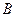 两种型号的电视参加了家电下乡活动,若厂家对
两种型号的电视参加了家电下乡活动,若厂家对 、
、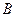 两种型号电视机的投放金额分别为
两种型号电视机的投放金额分别为 、
、 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为 、
、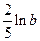 万元,已知
万元,已知 、
、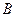 两种型号电视机的投放总金额为10万元,且
两种型号电视机的投放总金额为10万元,且 、
、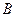 两种型号电视机的投放金额均不低于1万元.设这次活动中农民得到的补贴为
两种型号电视机的投放金额均不低于1万元.设这次活动中农民得到的补贴为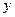 万元,写出
万元,写出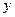 与
与 的函数关系式,并求补贴最多的方案.(精确到
的函数关系式,并求补贴最多的方案.(精确到 ,参考数据:
,参考数据: )
)
推荐套卷
某品牌电视生产厂家有 、
、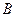 两种型号的电视参加了家电下乡活动,若厂家对
两种型号的电视参加了家电下乡活动,若厂家对 、
、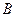 两种型号电视机的投放金额分别为
两种型号电视机的投放金额分别为 、
、 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为 、
、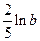 万元,已知
万元,已知 、
、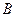 两种型号电视机的投放总金额为10万元,且
两种型号电视机的投放总金额为10万元,且 、
、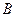 两种型号电视机的投放金额均不低于1万元.设这次活动中农民得到的补贴为
两种型号电视机的投放金额均不低于1万元.设这次活动中农民得到的补贴为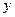 万元,写出
万元,写出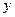 与
与 的函数关系式,并求补贴最多的方案.(精确到
的函数关系式,并求补贴最多的方案.(精确到 ,参考数据:
,参考数据: )
)