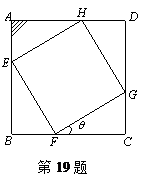
（本小题满分12分）如图所示，有块正方形的钢板ABCD，其中

首页 / 高中数学 / 试题详细

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 2093

（本小题满分12分）
如图所示，有块正方形的钢板ABCD，其中一个角有部分损坏,现要把它截成一块正方形的钢板EFGH. 在直角三角形GFC中，∠GFC =θ．若截后的正方形钢板EFGH的面积是原正方形钢板ABCD的面积的三分之二，求θ的值．

登录免费查看答案和解析

相关试题

已知，，且0＜茁＜琢＜，
（1）求的值.
（2）求.

题型：未知
难度：未知

收藏答案/解析

已知函数满足．
（1）求常数的值；
（2）解不等式．

题型：未知
难度：未知

收藏答案/解析

求曲线y=,,围成的平面图形的面积.

题型：未知
难度：未知

收藏答案/解析

已知p:方程有两个不相等的负实根；q:不等式的解集为R，若p∨q为真命题，p∧q为假命题，求m的取值范围。

题型：未知
难度：未知

收藏答案/解析

（本题12分）某地区上年度电价为元/kW•h，年用电量为 kW•h．本年度计划将电价降低到0．55元/ kW•h到0．75元/ kW•h之间，而用户期望电价为0．40元/ kW•h．经测算，下调电价后新增用电量与实际电价与用户的期望电价的差成反比（比例系数为），该地区电力的成本价为0．30元/ kW•h．
（1）写出本年度电价下调后，电力部门的收益与实际电价之间的函数关系式；
（2）设=，当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%？（注：收益=实际电量×（实际电价本价））

题型：未知
难度：未知

收藏答案/解析