(本小题满分12分)
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)用“五点法”在所给的直角坐标系中画出 在
在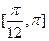 内的简图;
内的简图;
(3)函数 的图像经过怎样的平移伸缩变换使其对应的函数成为偶函数?
的图像经过怎样的平移伸缩变换使其对应的函数成为偶函数?
相关知识点
推荐套卷
(本小题满分12分)
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)用“五点法”在所给的直角坐标系中画出 在
在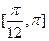 内的简图;
内的简图;
(3)函数 的图像经过怎样的平移伸缩变换使其对应的函数成为偶函数?
的图像经过怎样的平移伸缩变换使其对应的函数成为偶函数?