如图，在矩形地块ABCD中有两条道路AF，EC，其中AF是以A为顶点的抛物线段，EC是线段．AB=2km，BC=6km，AE=BF=4km．在两条道路之间计划修建一个花圃，花圃形状为直角梯形QPRE（线段EQ和RP为两个底边，如图所示）．求该花圃的最大面积．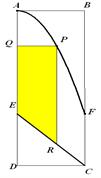
的大小
若
，求a的取值范围推荐套卷
如图，在矩形地块ABCD中有两条道路AF，EC，其中AF是以A为顶点的抛物线段，EC是线段．AB=2km，BC=6km，AE=BF=4km．在两条道路之间计划修建一个花圃，花圃形状为直角梯形QPRE（线段EQ和RP为两个底边，如图所示）．求该花圃的最大面积．
粤公网安备 44130202000953号