网络工程师是通过学习和训练,掌握网络技术的理论知识和操作技能的网络技术人员,他能够从事计算机信息系统的设计、建设、运行和维护工作.要获得网络工程师资格证书必须依次通过理论和操作两项考试,只有理论成绩合格时,才可继续参加操作的考试.已知理论和操作各只允许有一次补考机会,两项成绩均合格方可获得证书.现某人参加网络工程师证书考试,根据以往模拟情况,理论考试成绩每次合格的概率均为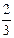 ,操作考试成绩每次合格的概率均为
,操作考试成绩每次合格的概率均为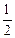 ,假设各次考试成绩合格与否均互不影响
,假设各次考试成绩合格与否均互不影响
(1)求他不需要补考就可获得网络工程师证书的概率;
(2)求他恰好补考一次就获得网络工程师证书的概率