本题满分10分)2010年6月11日,第十九届世界杯在南非拉开帷幕.比赛前,某网站组织球迷对巴西、西班牙、意大利、英格兰四支夺冠热门球队进行竞猜,每位球迷可从四支球队中选出一支球队,现有三人参与竞猜
(1)若三人中每个人可以选择任一球队,且选择各个球队是等可能的,求四支球队中恰好有两支球队有人选择的概率;
(2)若三人中有一名女球迷,假设女球迷选择巴西队的概率为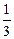 ,男球迷选择巴西队的概率为
,男球迷选择巴西队的概率为 ,记x为三人中选择巴西队的人数,求x的分布列和期望
,记x为三人中选择巴西队的人数,求x的分布列和期望
相关知识点
推荐套卷
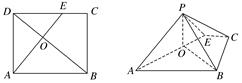
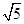 ,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=
,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=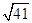 .
.
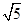 ,AB=AD=
,AB=AD=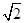 .将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).
.将图(1)沿直线BD折起,使得二面角ABDC为60°,如图(2).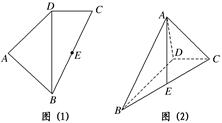
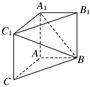
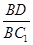 的值.
的值.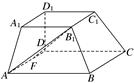

 粤公网安备 44130202000953号
粤公网安备 44130202000953号