（本小题满分13分）已知抛物线C：
与直线l：
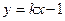没有公共点，设点P为直线l上的动点，过P作抛物线C的两条切线，A，B为切点．
（1）证明：直线AB恒过定点Q；
（2）若点P与（1）中的定点Q的连线交抛物线C于M，N两点，证明：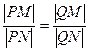
．
为钝角，且
，求
.
，求
的值
的取值范围
的值；
，求
的值
的对称点在单位圆
上，求椭圆的方程相关知识点
推荐套卷
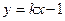（本小题满分13分）已知抛物线C：与直线l：没有公共点，设点P为直线l上的动点，过P作抛物线C的两条切线，A，B为切点．
（1）证明：直线AB恒过定点Q；
（2）若点P与（1）中的定点Q的连线交抛物线C于M，N两点，证明：．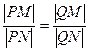
粤公网安备 44130202000953号