某公园准备建一个摩天轮,摩天轮的外围是一个周长为 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为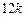 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为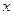 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为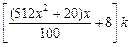 元,假设座位等距离分布,且至少有四个座位,
元,假设座位等距离分布,且至少有四个座位,
所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为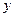 元.
元.
(Ⅰ)试写出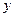 关于
关于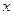 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(Ⅱ)当 米时,试确定座位的个数,使得总造价最低。
米时,试确定座位的个数,使得总造价最低。
相关知识点
推荐套卷
 在
在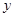 轴正半轴上,过点
轴正半轴上,过点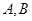 两点,线段
两点,线段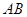 的长是
的长是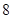 ,
,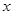 轴的距离是
轴的距离是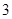 .
. ,使得过点
,使得过点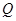 ,满足
,满足 ,且直线
,且直线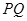 与抛物线在点
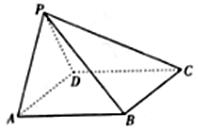
与抛物线在点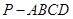 ,侧面
,侧面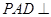 底面
底面 ,侧面
,侧面 为等边三角形,底面
为等边三角形,底面 .
.
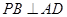 ;
;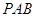 与平面
与平面 所成的角(锐角)的余弦值.
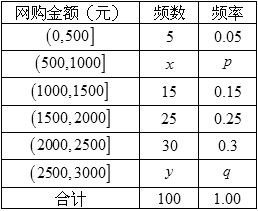
所成的角(锐角)的余弦值. 亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为
亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为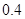 .
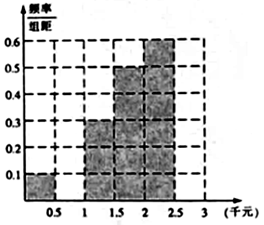
.
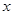 ,
, ,
,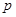 ,
, 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;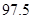 %的把握认为网购金额超过2000元与网龄在三年以上有关?
%的把握认为网购金额超过2000元与网龄在三年以上有关?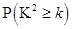

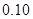

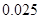
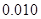
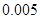
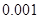
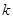


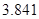


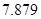

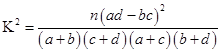 ,其中
,其中 )
)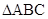 的内角
的内角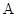 ,
,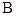 ,
,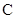 的对边分别为
的对边分别为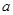 ,
,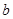 ,
,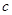 ,
,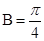 ,
,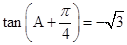 .
.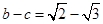 ,求
,求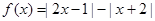 .
.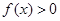 ;
;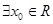 ,使得
,使得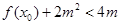 ,求实数
,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号