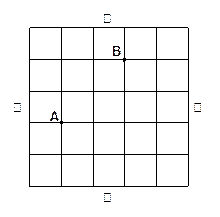如图是一个方形迷宫，甲、乙两人分别位于迷宫的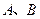
两处，两人同时以每一分钟一格的速度向东、西、南、北四个方向行走，已知甲向东、西行走的概率都为
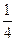，向南、北行走的概率为
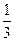和
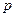，乙向东、西、南、北四个方向行走的概率均为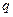
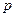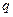⑴求和的值；
⑵问最少几分钟，甲、乙二人相遇？并求出最短时间内可以相遇的概率。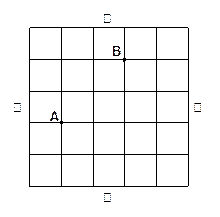
为实数，函数
，
的奇偶性；
与
的定义域是
且
,
,求
的定义域为
，且对任意
，都有
，且当
时，
恒成立，
（2）
的前
项和
，求数列推荐套卷
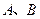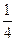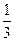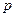如图是一个方形迷宫，甲、乙两人分别位于迷宫的两处，两人同时以每一分钟一格的速度向东、西、南、北四个方向行走，已知甲向东、西行走的概率都为，向南、北行走的概率为和，乙向东、西、南、北四个方向行走的概率均为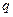
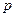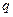⑴求和的值；
⑵问最少几分钟，甲、乙二人相遇？并求出最短时间内可以相遇的概率。
粤公网安备 44130202000953号