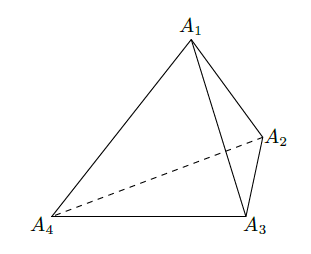
（1）如图，对于任一给定的四面体
，找出依次排列的四个相互平行的平面
，使得
（
=1,2,3,4），且其中每相邻两个平面间的距离都相等；
（2）给定依次排列的四个相互平行的平面
，其中每相邻两个平面间的距离为1，若一个正四面体
的四个顶点满足：
（
=1,2,3,4），求该正四面体
的体积.
相关试题
的前
项和为
，满足
，且
．
，
，
；
．
作抛物线的切线，求此切线方程；
的直线与抛物线
相交于两点
、
，抛物线
，试求点
满足
（
为虚数单位）．求
，当
时，
的极大值为7；当
时，
的值；
≥10)层，则每平方米的平均建筑费用为560+48
）推荐套卷
（1）如图，对于任一给定的四面体
，找出依次排列的四个相互平行的平面
，使得
（
=1,2,3,4），且其中每相邻两个平面间的距离都相等；
（2）给定依次排列的四个相互平行的平面
，其中每相邻两个平面间的距离为1，若一个正四面体
的四个顶点满足：
（
=1,2,3,4），求该正四面体
的体积.
粤公网安备 44130202000953号