为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中微量元素
的含量（单位：毫克）.下表是乙厂的5件产品的测量数据：
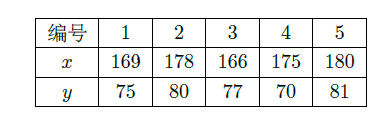
（1）已知甲厂生产的产品共98件，求乙厂生产的产品数量；
（2）当产品中的微量元素
满足
且
，该产品为优等品，用上述样本数据估计乙厂生产的优等品的数量；
（3）从乙厂抽出上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数
的分布列极其均值（即数学期望）。
（本小题共14分）在平面直角坐标系
中，椭圆
：
的一个顶点为
，离心率为
．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）直线
过点
，过
作的平行线交椭圆于P，Q两点，如果以PQ为直径的圆与直线相切，求的方程．
．
的极小值；
能否存在曲线
的切线，请说明理由．（本小题共14分）如图，在四棱锥S-ABCD中，底面ABCD为菱形，∠BAD=60°，平面SAD⊥平面ABCD，SA=SD，E，P，Q分别是棱AD，SC，AB的中点．
（Ⅰ）求证：PQ∥平面SAD；
（Ⅱ）求证：AC⊥平面SEQ；
（Ⅲ）如果SA=AB=2，求三棱锥S-ABC的体积．
（本小题共13分）某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据进行分组，分组区间为：[50,60），[60,70），[70,80），[80,90），[90,100]，并绘制出频率分布直方图，如图所示．
（Ⅰ）求频率分布直方图中的a值；从该市随机选取一名学生，试估计这名学生参加考试的成绩低于90分的概率；
（Ⅱ）设A，B，C三名学生的考试成绩在区间[80,90）内，M，N两名学生的考试成绩在区间[60,70）内，现从这5名学生中任选两人参加座谈会，求学生M，N至少有一人被选中的概率；
（Ⅲ）试估计样本的中位数落在哪个分组区间内 （只需写出结论）．
（注：将频率视为相应的概率）
，
．
的值；
在区间
上的最大值和最小值，及相应的x的值．
粤公网安备 44130202000953号