(本小题满分12分)函数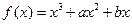 的图象C与x轴相切于不同于原点的一点,且
的图象C与x轴相切于不同于原点的一点,且 的极小值为-4。
的极小值为-4。
(I)求函数 的解析式及单调区间;
的解析式及单调区间;
(II)过曲线C上一点 (P1不是C的对称中心)作曲线C的切线,切C于不同于
(P1不是C的对称中心)作曲线C的切线,切C于不同于 的另一点
的另一点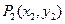 ,再过
,再过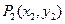 作曲线C的切线,切C于不同于
作曲线C的切线,切C于不同于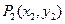 的另一点
的另一点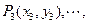 过
过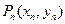 作曲线C的切线,切C于不同于
作曲线C的切线,切C于不同于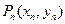 的另一点
的另一点 令
令 的通项公式。
的通项公式。
推荐套卷
(本小题满分12分)函数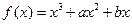 的图象C与x轴相切于不同于原点的一点,且
的图象C与x轴相切于不同于原点的一点,且 的极小值为-4。
的极小值为-4。
(I)求函数 的解析式及单调区间;
的解析式及单调区间;
(II)过曲线C上一点 (P1不是C的对称中心)作曲线C的切线,切C于不同于
(P1不是C的对称中心)作曲线C的切线,切C于不同于 的另一点
的另一点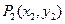 ,再过
,再过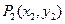 作曲线C的切线,切C于不同于
作曲线C的切线,切C于不同于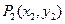 的另一点
的另一点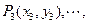 过
过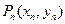 作曲线C的切线,切C于不同于
作曲线C的切线,切C于不同于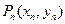 的另一点
的另一点 令
令 的通项公式。
的通项公式。