已知F是椭圆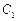
：
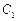＝1的右焦点，点P是椭圆上的动点，点Q是圆
：
＋
＝
上的动点．（1）试判断以PF为直径的圆与圆的位置关系；
（2）在x轴上能否找到一定点M，使得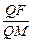
＝e (e为椭圆的离心率)？若存在，求出点M的坐标；若不存在，请说明理由．
、
异面直线，
为空间任一点，过
与
，且AB、CD在
。
、
，
，
，
为
中点，
，
，
，
，
，
，求：
为
中点。
推荐套卷
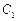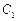已知F是椭圆：＝1的右焦点，点P是椭圆上的动点，点Q是圆：＋＝上的动点．（1）试判断以PF为直径的圆与圆的位置关系；
（2）在x轴上能否找到一定点M，使得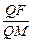＝e (e为椭圆的离心率)？若存在，求出点M的坐标；若不存在，请说明理由．
粤公网安备 44130202000953号