（本小题满分13分）某工厂对一批产品的质量进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图.已知样本中产品净重小于100克的个数是36个。
（I）求样本中净重在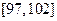
（克）的产品个数；
（II）若规定净重在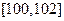
（克）的产品为一等品，依此抽样数据，求从该工厂随机抽取的3个产品中一等品个数
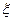的分布列和数学期望.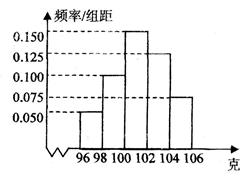
相关试题
中，角
为锐角,记角
所对的边分别为
，设向量
，且
与
的夹角为
．
的值并求角
，求
．
}的公差
，
，且
，
，
成等比数列．
及通项
的前
项和
中，角
所对的边分别为
，已知
,
，
．
的值；
的值．
,
的单调区间;
,不等式
恒成立，求
的取值范围．
的极值；
上的最大值和最小值．推荐套卷
（本小题满分13分）某工厂对一批产品的质量进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图.已知样本中产品净重小于100克的个数是36个。
（I）求样本中净重在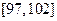（克）的产品个数；
（II）若规定净重在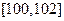（克）的产品为一等品，依此抽样数据，求从该工厂随机抽取的3个产品中一等品个数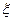的分布列和数学期望.
粤公网安备 44130202000953号