.如图1,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为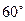 .
.
⑴求AO与BO的长;
⑵若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图2,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米;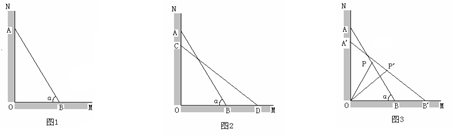 ②如图3,当A点下滑到A’点,B点向右滑行到B’点
②如图3,当A点下滑到A’点,B点向右滑行到B’点 时,梯子AB的中点P也随之运动到P’点.若∠POP’=
时,梯子AB的中点P也随之运动到P’点.若∠POP’=  ,求AA’的长和点P运动的路线长。
,求AA’的长和点P运动的路线长。
相关知识点
推荐套卷
.如图1,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为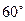 .
.
⑴求AO与BO的长;
⑵若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图2,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米; ②如图3,当A点下滑到A’点,B点向右滑行到B’点
②如图3,当A点下滑到A’点,B点向右滑行到B’点 时,梯子AB的中点P也随之运动到P’点.若∠POP’=
时,梯子AB的中点P也随之运动到P’点.若∠POP’=  ,求AA’的长和点P运动的路线长。
,求AA’的长和点P运动的路线长。