已知构成某系统的元件能正常工作的概率为p(0＜p＜1)，且各个元件能否正常工作是相互独立的．今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙．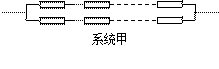
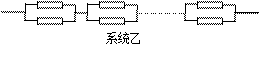
（1）试分别求出系统甲、乙能正常工作的概率p1，p2；
（2）比较p1与p2的大小，并从概率意义上评价两系统的优劣．
，对于满足
的一切
值都有
，求实数
的取值范围。
的值域；
，求
的值。
，且
。
的最大值，并求出相应的
、
的值。
一个周期的图象如图所示。 
的表达式；
，且A为△ABC的一个内角，求：
的值。
=1，
=2，
与
的夹角为60°。
，（
）·（
）；（2）求：
。推荐套卷
已知构成某系统的元件能正常工作的概率为p(0＜p＜1)，且各个元件能否正常工作是相互独立的．今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙．
（1）试分别求出系统甲、乙能正常工作的概率p1，p2；
（2）比较p1与p2的大小，并从概率意义上评价两系统的优劣．
粤公网安备 44130202000953号