（本大题共12分）
如图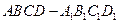
为正
方体，一只青蛙开始在顶点A处，它每次可随意
跳到相邻三顶点之一，若在五次内跳到
点，则停止跳动；若5次内不能跳到点，跳完五
次也停止跳动，求：
（1）5次以内能到点的跳法有多少种？
（2）从开始到停止，可能出现的跳法有多少种？
相关试题
在区间上
是增函数，求实数
的取值范围；
是
上的最大值和最小值.
（
，
）为偶函数，若对于任意
都有
成立，且
的最小值是为
．将函数
的图象向右平移
个单位后，得到函数
，求
的单调递减区间,确定其对称轴。
，
使等式
,
同时成立？若存在，求出
满足
，
，
，
，求
. 
，求证：
，若
为第二象限角，求
推荐套卷
（本大题共12分）
如图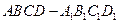 为正方体，一只青蛙开始在顶点A处，它每次可随意跳到相邻三顶点之一，若在五次内跳到点，则停止跳动；若5次内不能跳到点，跳完五次也停止跳动，求：
（1）5次以内能到点的跳法有多少种？
（2）从开始到停止，可能出现的跳法有多少种？
粤公网安备 44130202000953号