如右图所示，在三棱锥A－BCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．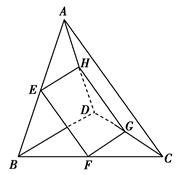
(1)求证：四边形EFGH是平行四边形；
(2)若AC＝BD，求证：四边形EFGH是菱形；
(3)当AC与BD满足什么条件时，四边形EFGH是正方形
，
，求
的值．
，集合
，求
．
是周期为
的周期函数吗？为什么？判断函数
是否为周期函数？
的等比数列
的首项
且满足
．
的前
项和
．
为等比数列，求这个数列的第
项．相关知识点
推荐套卷
如右图所示，在三棱锥A－BCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．
(1)求证：四边形EFGH是平行四边形；
(2)若AC＝BD，求证：四边形EFGH是菱形；
(3)当AC与BD满足什么条件时，四边形EFGH是正方形
粤公网安备 44130202000953号