某工厂拟建一座平面图(如右图所示)为矩形且面积为200平方米的三级污水处理池，由于地形限制，长、宽都不能超过16米，如果池外周壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元(池壁厚度忽略不计，且池无盖)．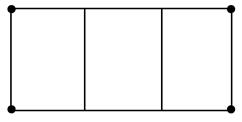
(1)写出总造价y(元)与污水处理池长x(米)的函数关系式，并指出其定义域；
(2)求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求最低总造价．
相关试题
在（
）处的切线方程为
。
的表达式；
满足什么条件时，函数
上单调递增？
。
的极大值点与极小值点；
上的最大值与最小值。
满足
，且
在区间
和区间
上分别单调。
求
的值。
的不等式
<0的解集为
，函数
的定义域为
。
，求集合
，求正数
的取值范围。
，证明：当
时，
；
。证明：
。推荐套卷
某工厂拟建一座平面图(如右图所示)为矩形且面积为200平方米的三级污水处理池，由于地形限制，长、宽都不能超过16米，如果池外周壁建造单价为每米400元，中间两条隔墙建造单价为每米248元，池底建造单价为每平方米80元(池壁厚度忽略不计，且池无盖)．
(1)写出总造价y(元)与污水处理池长x(米)的函数关系式，并指出其定义域；
(2)求污水处理池的长和宽各为多少时，污水处理池的总造价最低？并求最低总造价．
粤公网安备 44130202000953号