某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组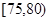 ,第2组
,第2组 ,第3组
,第3组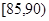 ,第4组
,第4组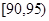 ,第5组
,第5组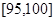 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示
(1)分别求第3,4,5组的频率;
(2)若该校决定在第3,4,5 组中用分层抽样的方法抽取6名学生进入第二轮面试,
①已知学生甲和学生乙的成绩均在第3组,求学生甲和学生乙同时进入第二轮面试的概率;
②学校决定在这6名学生中随机抽取2名学生接受考官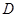 的面试,第4组中有
的面试,第4组中有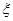 名学生被考官
名学生被考官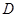 面试,求
面试,求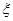 的分布列和数学期望.
的分布列和数学期望.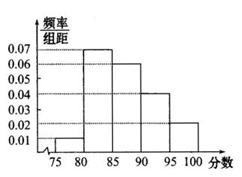
相关知识点
推荐套卷
 ,F是BC的中点.
,F是BC的中点.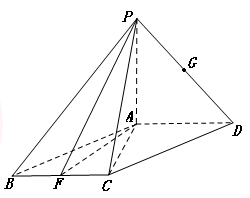
 是等比数列,
是等比数列, ,且
,且 是
是 的等差中项.
的等差中项.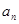 ;
;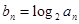 ,求数列
,求数列 的前n项和
的前n项和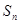 .
. 中,
中,
 的值 ;(Ⅱ)求
的值 ;(Ⅱ)求 的值。
的值。 .
. 在
在 和
和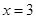 处的切线互相平行,求
处的切线互相平行,求 的值;
的值; 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 中,点
中,点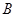 与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于
与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于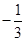 .
.
 交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。 粤公网安备 44130202000953号
粤公网安备 44130202000953号