(本小题满分16分)
已知数列﹛an﹜中,a2=p(p是不等于0的常数),Sn为数列﹛an﹜的前n项和,若对任意的正整数n都有Sn= .
.
(1)证明:数列﹛an﹜为等差数列;
(2)记bn= +
+ ,求数列﹛bn﹜的前n项和Tn;
,求数列﹛bn﹜的前n项和Tn;
(3)记cn=Tn-2n,是否存在正整数m,使得当n>m时,恒有cn∈(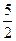 ,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
推荐套卷
(本小题满分16分)
已知数列﹛an﹜中,a2=p(p是不等于0的常数),Sn为数列﹛an﹜的前n项和,若对任意的正整数n都有Sn= .
.
(1)证明:数列﹛an﹜为等差数列;
(2)记bn= +
+ ,求数列﹛bn﹜的前n项和Tn;
,求数列﹛bn﹜的前n项和Tn;
(3)记cn=Tn-2n,是否存在正整数m,使得当n>m时,恒有cn∈(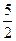 ,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。