（本小题满分14分）
如图，在半径为R、圆心角为
的扇形金属材料中剪出一个长方形EPQF，并且EP与∠AOB的平分线OC平行，设∠POC=θ.
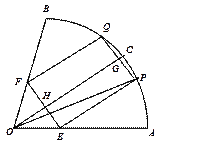
（1）将θ表示为长方形EPQF的面积S（θ）的函数
（2）现用EP和FQ作为母线并焊接起来，将长方形EPQF制成圆柱的侧面，能否从△OEF中直接剪出一个圆面作为圆柱形容器的底面？如果不能，请说明理由；如果能，求出侧面积最大时圆柱形容器的体积.
的偶函数
. 
的值; 
的单调性;
对任意
恒成立，求实数
的取值范围.
,其中
.
,求函数f(x)的最小正周期；
满足
,且
,求函数f(x)的单调递减区间.
,
,求
的值；
.求
的值.
;
.
；
，求
,
。相关知识点
推荐套卷
（本小题满分14分）
如图，在半径为R、圆心角为的扇形金属材料中剪出一个长方形EPQF，并且EP与∠AOB的平分线OC平行，设∠POC=θ.
（1）将θ表示为长方形EPQF的面积S（θ）的函数
（2）现用EP和FQ作为母线并焊接起来，将长方形EPQF制成圆柱的侧面，能否从△OEF中直接剪出一个圆面作为圆柱形容器的底面？如果不能，请说明理由；如果能，求出侧面积最大时圆柱形容器的体积.
粤公网安备 44130202000953号