本小题满分14分）
三次函数
的图象如图所示，直线BD∥AC，且直线BD与函数图象切于点B，交于点D，直线AC与函数图象切于点C，交于点A．
（1）若函数f(x)为奇函数且过点（1，-3），当x<0时求
的最大值 ；
（2）若函数在x=1处取得极值-2，试用c表示a和b，并求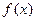
的单调递减区间；
（3）设点A、B、C、D的横坐标分别为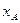
，
，
，
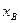求证
；
的一切实数m都成立，求x的取值范围。
的定义域为R，值域[0，2]，求实数m与n的值。
B=
）∩B=B，求实数a的取值范围。
．
,求a的取值范围；
．
推荐套卷
本小题满分14分）
三次函数的图象如图所示，直线BD∥AC，且直线BD与函数图象切于点B，交于点D，直线AC与函数图象切于点C，交于点A．
（1）若函数f(x)为奇函数且过点（1，-3），当x<0时求的最大值 ；
（2）若函数在x=1处取得极值-2，试用c表示a和b，并求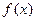的单调递减区间；
（3）设点A、B、C、D的横坐标分别为，，，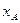
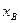求证；
粤公网安备 44130202000953号