(1)(本小题满分7分) 选修4一2:矩阵与变换
若点A(2,2)在矩阵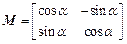 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵.
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵.
(2)(本小题满分7分) 选修4一4:坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合,极轴与x轴的正半轴重合,曲线C1: 与曲线C2:
与曲线C2: (t∈R)交于A、B两点.求证:OA⊥OB.
(t∈R)交于A、B两点.求证:OA⊥OB.
(3)(本小题满分7分) 选修4一5:不等式选讲
求证: ,
, .
.
推荐套卷
(1)(本小题满分7分) 选修4一2:矩阵与变换
若点A(2,2)在矩阵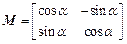 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵.
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵.
(2)(本小题满分7分) 选修4一4:坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合,极轴与x轴的正半轴重合,曲线C1: 与曲线C2:
与曲线C2: (t∈R)交于A、B两点.求证:OA⊥OB.
(t∈R)交于A、B两点.求证:OA⊥OB.
(3)(本小题满分7分) 选修4一5:不等式选讲
求证: ,
, .
.