（本小题12分）
如图，
＜
＜
＜…＜
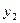）是曲线C
：
上的n个点，点
在x轴的正半轴上，且⊿
是正三角形（
是坐标原点）。
（1）写出
(2)求出点
的横坐标
关于n的表达式并用数学归纳法证明
为空间四边形
的边
上的点，且
，求证：
的底面是边长为1的正方形，
平面
是平行四边形
所在平面外一点，
、
分别是
、
的中点； 求证：
平面
平面
，
直线
，则
平面
经过平面
内一定点
，但相关知识点
推荐套卷
（本小题12分）
如图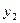，＜＜＜…＜）是曲线C：上的n个点，点在x轴的正半轴上，且⊿是正三角形（是坐标原点）。
（1）写出
(2)求出点的横坐标关于n的表达式并用数学归纳法证明
粤公网安备 44130202000953号