一个袋中有10个大小相同的黑球、白球和红球，已知从袋中任意摸出一个球，得到黑球的概率是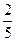
；从袋中任意摸出2个球，至少得到1个白球的概率是
（1）求袋中白球的个数；
（2）若将其中的红球拿出，从剩余的球中一次摸出3个球，求恰好摸到2个白球的概率；
（3）在（2）的条件下，一次摸出3个球，求取得白球数X的数学期望。
相关试题
是矩形，
平面
，
是
上一点，
平面
，点
，
分别是
的中点. 
平面
.
，
，函数
. 
的最小正周期和最大值；
上的最大值和最小值.
在
上为增函数，求实数
的取值范围
时，求
上的最大值和最小值
，
恒成立
，若数列
，
满足
，
，
，
的关系，并求数列
， 若
恒成立．求
的最小值．
与抛物线
交于不同两点A、B，F为抛物线的焦点。
的重心G的轨迹方程；
的外接圆的方程。推荐套卷
一个袋中有10个大小相同的黑球、白球和红球，已知从袋中任意摸出一个球，得到黑球的概率是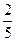；从袋中任意摸出2个球，至少得到1个白球的概率是
（1）求袋中白球的个数；
（2）若将其中的红球拿出，从剩余的球中一次摸出3个球，求恰好摸到2个白球的概率；
（3）在（2）的条件下，一次摸出3个球，求取得白球数X的数学期望。
粤公网安备 44130202000953号